前回はファイナンスの入門って感じで割ととっつきやすい内容だったが、今回からぐっとファイナンスっぽくなってくる。

投資には「リスク」が付き物だ。リスクとは「危機」。"危険"と"機会"の2つの性質を併せ持つ。ファイナンスの力で、この「リスク」を定量化してどこにどれくらいの割合で投資すると最大のリターンが来るのかを求めたいっていうのが、今回のゴール。
統計入門
このリスクの定量化には統計の知識が必要。なのでまずはざっと解説。
標準偏差と分散
たくさんのデータの「ばらつき」を数値で表現。 かっこよく言うと、「ボラティリティ」
式を一般化する途端に拒絶反応を起こす人が多い(自分含)ので、具体例で解説。
例)3つの数値がある。これをX1, X2, X3 とし、平均をXとすると、標準偏差は以下のように表される。
標準偏差 = √分散 = √ ( (X1 - X)^2 + (X2 - X)^2 + (X3 - X)^2) / 3
ここで、標準偏差が大きいほど、そのばらつきが多いことになる。株式投資においては、これが「リスクが高い」と言える。EXCELを使えば、一発で計算できる関数がある。
正規分布
データの値の数を Y軸、データの値の範囲をX軸に置くと、大体以下のようなグラフになる。

ここで大事なのが、68.26%, 95.44% といった値。これの意味を知ろう。 ちなみに図中のμが平均、ρが標準偏差だ。
例)平均が150で分散が10
- 140 ~ 160 が全体の68.26%に含まれる。
- 130 ~ 170 が全体の95.44%に含まれる。
ちなみにご存知の"偏差値"は平均点を50点にし、標準偏差を10になるように変換したもの。
つまり、偏差値70以上の人間は、 (100 - 95.44) / 2 = 2.28(%) ということになる。
変動係数
平均から 68% の範囲になるのはいくらか、を出す為の係数。
変動係数 = ρ(標準偏差) / μ(平均) * 100
この変動係数が今後の予想に使える。
例えば平均が780, 標準偏差が50 だとする。 すると、 50 / 780 * 100 = 6.41。
次年度の予想価格が820の場合、 820 * 6.41(%) = 52.56。つまり、68%の確率で、 767から 872の範囲になる。といった具合。
共分散
投資のリスクを考える際、他の株式等の相関の度合いを見て投資判断をする必要がある。マーケットの市場の指標がこれだけ上がると、あの株価もあれだけ上がるみたいな感覚。
AとBの共分散の求め方
- AとBの株式の時期別の偏差 (リターンと平均値の差)を計算し、2つを掛ける。
- それらの平均値を出す。つまり、全部足してその数分だけ割る
共分散は正負に注目!これがプラスなら A のリターンが平均を超える時は、Bのリターンも平均より良いことを表す。 共分散は2つの相関の強さを表している訳では無い点に注意。つまり、共分散が高くても2つは似ているとは言い切れない。
EXCEL におけるCORVAR 関数で一発計算。
相関係数
2つの相関を求める。
AとBの相関係数の求め方
- AとBの共分散を算出
- 共分散をAとBの標準偏差の積で割る
相関係数がプラスの場合: Aが増えればBも増え、Aが減ればBも減る割合が高い
相関係数がゼロの場合: AとBには特に関係がない
相関係数の目安
- ± 0.7 ~ ±1.0 : 強い相関
- ± 0.4 ~ ±0.7 : 中程度の相関
- ± 0.2 ~ ±0.4 : 弱い相関
- ± 0.0 ~ ±0.2 : ほとんど相関が無い
もちろんEXCELに関数が用意されてるので、これを使う。 CORREL関数
ポートフォリオによる分散投資
さて、株式投資の世界では「どの株をどれくらいの割合で持ってれば良いのか」という考えが大事。これをポートフォリオという。
ポートフォリオの期待収益率
それぞれの期待収益率の加重平均で求める。
※期待収益率とは、予想される収益率分布の期待値を指す。例えばある株式の利回りを30% の確率で+4%, 30%の確率で+2%, 40%の確率で -2%としている場合、 4 * 30% + 2 * 30% - 2 * 40% = 1.0% となる。
例)コカコーラの平均収益率 : 12.54 % , 株所有比率 40%, IBM の平均収益率: 28.66% , 所有比率 60%。平均収益率は月次or年次の株価の変動の割合の平均。平均収益率が高ければいいと言う訳ではない。それだけリスクがある。
コカコーラとIBMのポートフォリオの期待収益率 = 12.54 % * 40 / 100 + 28.66% * 40 / 100 = 22.21 %
期待収益率により、"リスクはどうであれ、その割合で投資すればどのくらいの収益が見込めるか" がわかる。ここで、リスクがわかれば 「できるだけ低いリスクで最大の収益率が見込めるものはどれか」っていう合理的な選択ができる。
ポートフォリオの分散
AとBの分散を求める。ちょいと複雑。こういうモンだと思った方が良い。
(Ax + By)^2 = A^2X^2 + B^2Y^2 + 2ABXY みたいな感じ
AとBの分散 = (Aの投資率)^2 * (Aの分散) + (Bの投資率)^2 * (Bの分散) + 2 * (Aの投資率) * (Bの投資率) * (共分散)
さて、これでAとBにおける投資割合に応じたリスクが求められる。X軸をリスク(標準偏差), Y軸を期待収益率にして各株式の保有割合を変えてグラフにプロットしてみよう。以下のようになる。ファイナンス界では超有名なグラフ。
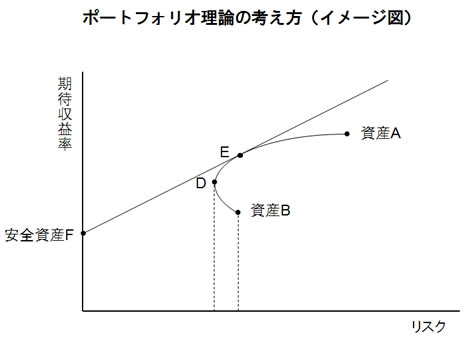
とりあえず直線は無視して、曲線に注目。プロットすると上記のような曲線になる。
さて、ここで点Dに注目。これより下にある曲線状の点は、「同じリスクなのに、期待収益率が低い」ゾーンとなっている。資産B の位置は「Aの保有率0%, Bの保有率100%」の場合の点だ。その点の真上にもう一個点が打てる。その点も同じリスクなのに、期待収益率が高い!だからBだけを100%保有するのはアホの選択ということになる。この点Dより上のエリアのことを「効率的フロンティア」と呼ぶ。
効率的フロンティア内でどれを選択するか。それは投資家のリスク許容割合に応じて決められる。リスクとっていいなら、資産Aに100%投資すれば良い。
リスクフリー資産を合わせる
国債などのリスクの無い資産(リスクフリー資産)を組み合わせることで、"同じリスクで最大の収益が上げられるポートフォリオ"という夢のような組み合わせが求められる。
それが前図における安全資産Fだ。点Fが意味するのは、「国債に100%投資した場合の収益率」だ。これはリスクがゼロで例えば3%の収益率が期待できる。
ここでポートフォリオの特徴として「リスクフリー資産をポートフォリオに組み込んだとたん、リスクとリターンの関係が直線になる」という特徴がある。そういうモンだと思おう。
そしてこのリスクフリー資産を原点とした直線で、ポートフォリオのグラフとの接点、これこそが「同じリスクで最大の収益が上げられるポートフォリオ」となるのだ!この素晴らしい線を「資本市場線」と呼び、接点である図中の点E を「マーケットポートフォリオ」という。
点E は(仮にAに60%、B に40%とする) が100% , 国債に0% 投資した際の点だ。この直線上を左下にいくにつれて、(Aに60%, Bに40%) に投資する割合が減って、国債に投資する割合が増える場合となる。 逆に右上に行くに連れて、リスクフリーレート(国債と同じ利息2%)で借り入れをして、その借り入れた分を (Aに60%, Bに40%)に全額投資することになる。 この線上でどの点を選ぶかは投資家のリスク許容の範囲次第。ただこの線上から選ぶのが同じリスクで最大の収益が得られる選択となる。
マーケットポートフォリオを求める
さて、この"マーケットポートフォリオ(点E)" をどうやって求めれば良いのだろう? それさえわかれば、Aの投資割合、Bの投資割合が決まって、後はリスク許容の割合次第で国債に投資するということができる。
これを知るには、シャープレシオという言葉が関わって来る。これは「ポートフォリオがリスクに見合った運用実績を上げているかを見る指標」だ。
シャープレシオ = リスクプレミアム (ポートフォリオの期待リターン - リスクフリー・レート) / ポートフォリオのリスク (標準偏差)
数学的に言えば、これは一次関数の「傾き」を求める式と一緒だ。このシャープレシオが最大になるようなポートフォリオこそ、マーケットポートフォリオ(点E)となる。これはエクセルのソルバーという機能を使って求めることができる。
マーケットリスクの考慮
上記で求めたポートフォリオの欠点として、市場全体のリスクを考えられていない点がある。例えば景気、金利、為替の動向などや企業そのもの、業界に関連したリスクだ。これらは分散化によっても取り除くことができないリスクとなる。これを何とか考慮すれば、まさに最強のポートフォリオができるんじゃないか。それを考える上でβ(ベータ)の考えが必要。
β ・・・ 市場全体の指標(TOPIX) が増加すると、対象の銘柄はいくつ増加or減少するか。分散化によって取り除くことができない市場リスクを測るモノサシ
このβの値は各企業によって異なる。これは過去のTOPIXとその企業の統計より導きだされる。それぞれのプロットした点に一番フィットする直線の傾きがβ。
CAPM 資本資産評価モデル(Capital Asset Pricing Model)
資産i の期待リスクプレミアム = β * マーケットのリスクプレミアム
つまりβの値が小さければ、資産iのリスクプレミアムはマーケット全体のリスクプレミアムより小さくなるし、大きければ資産iのリスクプレミアムはマーケット全体のリスクプレミアムより大きくなる。
例) 国債(リスクフリー・レート)1%、マーケットポートフォリオの期待収益率: 5%, 企業Aのβ: 1.5% の時のAの期待収益率
(X- 1%) = 1.5% * (5% - 1%) X = 7%
このようにして、企業Aのマーケットリスクを加味した期待収益率を求めることができる。
CAPMを一般化してみる。資産iの期待収益率 を R, マーケットの期待収益率をrf, リスクフリーレートをri とする
(R - ri) = β * (rf - ri) R = (rf -ri)β + ri
すると、下記のようなグラフができる。
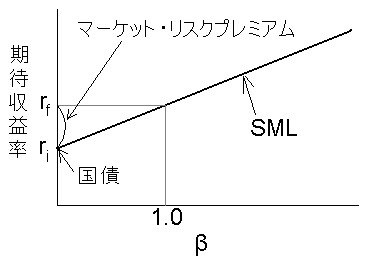
ここで、 (m-ri) の傾きを証券市場線といい、マーケット全体を表す傾きとなる。こうして一般化すれば、企業のβがわかれば、その企業の期待収益率が求められる。それを元にしてポートフォリオを組むことで、市場を加味した素晴らしいマーケットポートフォリオが出来上がる。